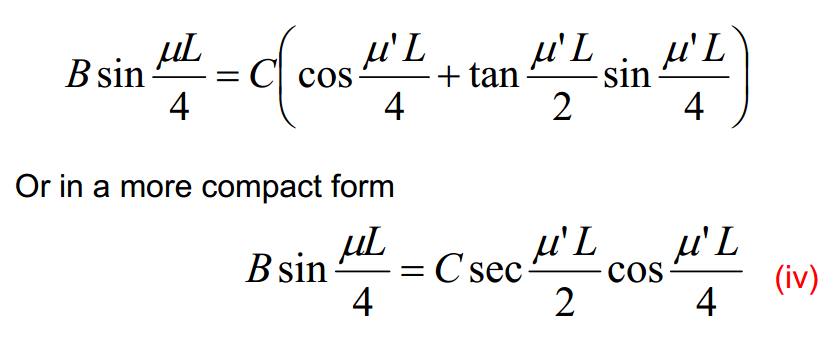The expression1−cotAtanA​+1−tanAcotA​ can be written as.If 0≤xLet p,q and rr be the sides opposite to the angles P,Q and R, respectively….The number of solutions of 2sinx+cosx=3 is….….​.If sinθ=1+t22t​ and ? lies in the second quadrant, then cosθ ….​.The formula for sin, cos and tan can be represented as follows. These can be represented in terms of the sides (opposite side, adjacent side and hypotenuse) respective to the angle of a right-angled triangle. Sin, Cos and Tan are the abbreviated forms of Sine, Cosine and Tangent respectively. Sin, Cos and Tan are the basic trigonometric ratios used to examine the relationship between the angles and sides of a triangle (especially of a right-angled triangle).